NumPy reshape(): How to Reshape NumPy Arrays in Python

In this educational, you’ll learn the way to use NumPy reshape() to reshape NumPy arrays with out converting the unique information.

When running with Numpy arrays, chances are you’ll continuously need to reshape an present array into an array of various dimensions. This can also be in particular helpful while you develop into information in more than one steps.

And NumPy reshape() is helping you do it simply. Over the following few mins, you’ll be told the syntax to use reshape(), and likewise reshape arrays to other dimensions.

What is Reshaping in NumPy Arrays?

When running with NumPy arrays, chances are you’ll first need to create a 1-dimensional array of numbers. And then reshape it to an array with the required size.

This is especially useful when the scale of the brand new array don’t seem to be recognized first of all or are inferred all through execution. Or it can be conceivable {that a} sure information processing step calls for the enter to be of a selected form.

Here’s the place reshaping comes in to hand.

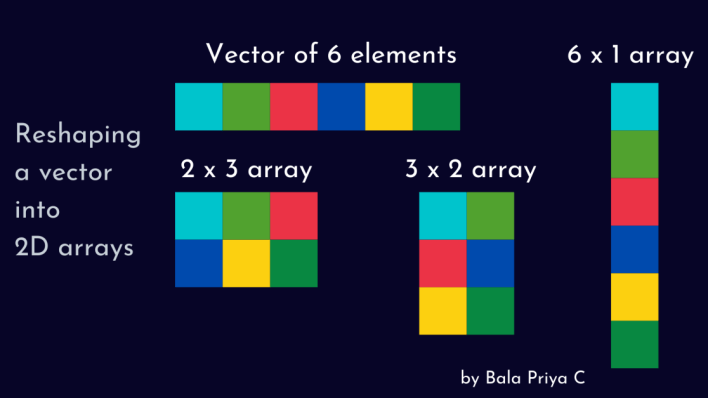
For instance, believe the next representation. We have a vector—a one-dimensional array of 6 components. And we will be able to reshape it into arrays of shapes 2×3, 3×2, 6×1, and so forth.

▶️ To observe in conjunction with the examples in this educational, you wish to have to have Python and NumPy put in. If you don’t have NumPy but, take a look at our NumPy set up information.

You might now cross forward and import NumPy underneath the alias np, by means of operating: import numpy as np.

Let’s continue to be told the syntax in the following segment.

Syntax of NumPy reshape()

Here’s the syntax to use NumPy reshape():

np.reshape(arr, newshape, order = 'C'|'F'|'A')

• arr is any legitimate NumPy array object. Here, it’s the array to be reshaped.
• newshape is the form of the brand new array. It can also be both an integer or a tuple.
• When newshape is an integer, the returned array is one-dimensional.
• order refers to the order in which you’d like to learn in the weather of the array to be reshaped.
• The default price is ‘C’, which means that the weather of the unique array shall be learn in a C-like indexing order (beginning with 0)
• ‘F’ stands for Fortran-like indexing (beginning with 1). And ‘A’ reads in the weather in both C-like or Fortran-like order relying at the reminiscence format of the array arr.

So what does np.reshape() go back?

It returns a reshaped view of the unique array if conceivable. Else, it returns a replica of the array.

In the above line, we discussed that NumPy reshape() would take a look at to go back a view on every occasion conceivable. Else, it returns a replica. Let’s continue to speak about the variations between a view and a duplicate.

View vs. Copy of NumPy Arrays

As the title suggests, replica is a duplicate of the unique array. And any adjustments made to the replica will now not have an effect on the unique array.

On the opposite hand, view merely refers to reshaped view of the unique array. This implies that any exchange made to the view may also have an effect on the unique array and vice versa.

Use NumPy reshape() to Reshape 1D Array to 2D Arrays

#1. Let’s get started by means of developing the pattern array the use of np.arange().

We want an array of 12 numbers, from 1 to 12, known as arr1. As the NumPy arange() serve as excludes the endpoint by means of default, set the forestall price to 13.

Now allow us to use the above syntax, and reshape arr1 with 12 components right into a 2D array of form (4,3). Let’s name this arr2 with 4 rows, and three columns.

import numpy as np

arr1 = np.arange(1,13)
print("Original array, ahead of reshaping:n")
print(arr1)

# Reshape array
arr2 = np.reshape(arr1,(4,3))
print("nReshaped array:")
print(arr2)

Let’s check out the unique and reshaped arrays.

Original array, ahead of reshaping:

[ 1  2  3  4  5  6  7  8  9 10 11 12]

Reshaped array:
[[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 11 12]]

Instead of passing in the array as a controversy np.reshape(), you’ll additionally name the .reshape() way at the unique array.

You can run dir(arr1), and it’s going to record down all of the conceivable strategies and attributes that you’ll use at the array object arr1.

dir(arr1)

# Output 
[
...
...
'reshape'
...
..
]

In the above code mobile, you’ll see that .reshape() is a legitimate way to use at the present NumPy array arr1.

▶️ So, you’ll additionally use the next simplified syntax to reshape NumPy arrays.

arr.reshape(d0,d1,...,dn)

# the place:

# d0, d1,..,dn are the scale of the reshaped array

# d0 * d1 * ...* dn = N, the collection of components in arr

For the remainder of this educational, allow us to use this syntax in our examples.

#2. Let’s take a look at reshaping our 12-element vector right into a 12 x 1 array.

import numpy as np

arr1 = np.arange(1,13)
print("Original array, ahead of reshaping:n")
print(arr1)

# Reshape array
arr3 = arr1.reshape(12,1)
print("nReshaped array:")
print(arr3)

In the output under, you’ll see that the array has been reshaped as wanted.

Original array, ahead of reshaping:

[ 1  2  3  4  5  6  7  8  9 10 11 12]

Reshaped array:
[[ 1]
 [ 2]
 [ 3]
 [ 4]
 [ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]
 [11]
 [12]]

❔ So, how will we test if now we have got a duplicate or a view?

To test this, you’ll name the base characteristic at the returned array.

• If the array is a duplicate, the base characteristic shall be None.
• If the array is a view, the base characteristic would be the unique array.

Let’s temporarily examine this.

arr3.base
# Output
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

As you’ll see, base characteristic of arr3 returns the unique array. This implies that we’ve gained a view of the unique array.

#3. Now, let’s take a look at to reshape the vector into every other legitimate 2 x 6 array.

import numpy as np

arr1 = np.arange(1,13)
print("Original array, ahead of reshaping:n")
print(arr1)

# Reshape array
arr4 = arr1.reshape(2,6)
print("nReshaped array:")
print(arr4)

And right here’s the output:

Original array, ahead of reshaping:

[ 1  2  3  4  5  6  7  8  9 10 11 12]

Reshaped array:
[[ 1  2  3  4  5  6]
 [ 7  8  9 10 11 12]]

In the following segment, let’s reshape arr1 right into a 3-D array.

Use NumPy reshape() to Reshape 1D Array to 3-D Arrays

To reshape arr1 to a 3-D array, allow us to set the required dimensions to (1, 4, 3).

import numpy as np

arr1 = np.arange(1,13)
print("Original array, ahead of reshaping:n")
print(arr1)

# Reshape array
arr3D = arr1.reshape(1,4,3)
print("nReshaped array:")
print(arr3D)

We’ve now created a 3-D array with the similar 12 components as the unique array arr1.

Original array, ahead of reshaping:

[ 1  2  3  4  5  6  7  8  9 10 11 12]

Reshaped array:
[[[ 1  2  3]
  [ 4  5  6]
  [ 7  8  9]
  [10 11 12]]]

How to Debug Value Errors During Reshaping

If you keep in mind the syntax, reshaping is legitimate best when the fabricated from the scale is equivalent to the collection of components in the array.

import numpy as np

arr1 = np.arange(1,13)
print("Original array, ahead of reshaping:n")
print(arr1)

# Reshape array
arr2D = arr1.reshape(4,4)
print("nReshaped array:")
print(arr2D)

Here, you’re attempting to reshape a 12-element array right into a 4×4 array with 16 components. The interpreter throws a Value Error, as observed under.

Original array, ahead of reshaping:

[ 1  2  3  4  5  6  7  8  9 10 11 12]
-----------------------------------------------------------
ValueError                                
Traceback (most up-to-date name ultimate)
<ipython-input-11-63552bcc8c37> in <module>()
      6 
      7 # Reshape array
----> 8 arr2 = arr1.reshape(4,4)
      9 print("nReshaped array:")
     10 print(arr2)

ValueError: can't reshape array of measurement 12 into form (4,4)

To keep away from such mistakes, chances are you’ll use -1 to the robotically infer the form for probably the most dimensions—in line with the whole collection of components.

For instance, if you recognize n – 1 dimensions previously, you’ll use -1 to infer the n-th size in the reshaped array.

If you might have a 24-element array and you desire to to reshape it right into a 3-D array. Suppose you wish to have 3 rows and four columns. You can go in the worth of -1 alongside the 3rd size.

import numpy as np

arr1 = np.arange(1,25)
print("Original array, ahead of reshaping:n")
print(arr1)

# Reshape array
arr_res = arr1.reshape(4,3,-1)
print("nReshaped array:")
print(arr_res)
print(f"Shape of arr_res:arr_res.form")

When you read about the form of the form array, you’ll see that the reshaped array has a form of two alongside the 3rd size.

Original array, ahead of reshaping:

[ 1  2  3  4  5  6  7  8  9 10 11 12 
13 14 15 16 17 18 19 20 21 22 23 24]

Reshaped array:
[[[ 1  2]
  [ 3  4]
  [ 5  6]]

 [[ 7  8]
  [ 9 10]
  [11 12]]

 [[13 14]
  [15 16]
  [17 18]]

 [[19 20]
  [21 22]
  [23 24]]]
Shape of arr_res:(4, 3, 2)

This is especially useful in pulling down an array. And you’ll know about that in the following segment.

Use NumPy reshape() to Flatten an Array

There are occasions while you’d want to return from N-dimensional arrays to a flattened array. Suppose you wish to have to flatten a picture into a protracted vector of pixels.

Let’s code a easy instance the use of the next steps:

• Generate a three x 3 grayscale symbol array, img_arr—with pixels in the variability 0 to 255.
• Next, flatten this img_arr and print out the flattened array, flat_arr.
• Also, print out the shapes of img_arr and flat_arr to examine.

img_arr = np.random.randint(0, 255, (3,3))
print(img_arr)
print(f"Shape of img_arr: img_arr.form")
flat_arr = img_arr.reshape(-1)
print(flat_arr)
print(f"Shape of flat_arr: flat_arr.form")

Here’s the output.

[[195 145  77]
 [ 63 193 223]
 [215  43  36]]
Shape of img_arr: (3, 3)

[195 145  77  63 193 223 215  43  36]
Shape of flat_arr: (9,)

In the above code mobile, you’ll see that flat_arr is a 1D vector of pixel values with 9 components.

Summing Up👩‍🏫

It’s time to temporarily overview what now we have discovered.

• Use np.reshape(arr, newshape) to reshape arr into the form specified in newshape. newshape is a tuple specifying the scale of the reshaped array.
• Alternatively, use arr.reshape(d0, d1, …, dn) to reshape arr to be of form d0 x d1 x … x dn
• Check if d0 * d1 * …* dn = N, the collection of components in the unique array, to keep away from Value Errors all through reshaping.
• Use -1 for at maximum one size in the brand new form if you need the size to be robotically inferred.
• Finally, chances are you’ll use arr.reshape(-1) to flatten the array.

Now that you know the way to use NumPy reshape(), learn the way the NumPy linspace() serve as works.

You might check out the code examples in Jupyter pocket book if you happen to’d like. If you’re searching for different construction environments, take a look at our information on Jupyer choices.